# 计量经济学
# 引论
# 计量经济学的用途
描述经济现实:
将经济关系中的抽样符号定量化,如需求函数、消费倾向;
检验经济理论假设:
采用现实证据来检验理论模型,如资本资产定价模型、有效市场假说;
预测未来经济活动:
基于已发生的事件去预测未来,如 GDP、CPI、通货膨胀率等;
# 计量经济学的研究路线
- 建立理论模型
- 确定计量经济学模型
- 收集、检查并整理数据
- 估计计量经济学模型
- 评价计量经济学模型
- 应用计量经济学模型
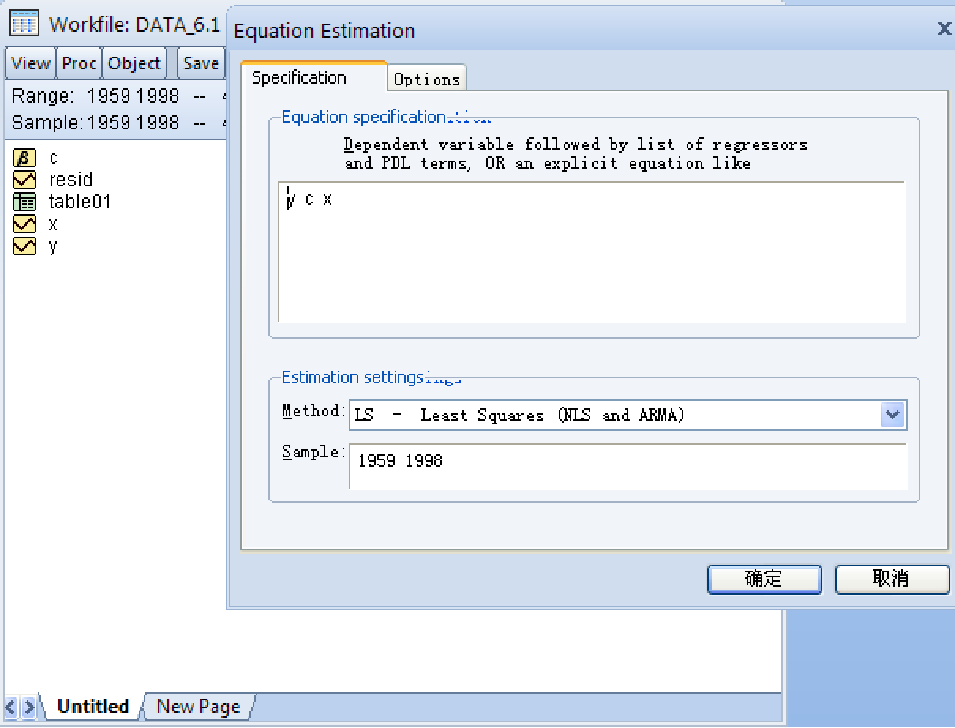
# EViews 使用
# 第一章 回归分析概述
# 回归意义


统计关系
确定关系:确定变量之间的函数关系
统计关系:随机变量之间的依赖关系
计量经济学研究的是统计关系。
# 回归与相关
回归与相关的基本不同点在于,回归分析将因变量当作统计的、随机的,而自变量则被看作是固定的或非随机的;而相关分析将两个变量都看作随机的,具有对称性;
事实上,将自变量看作是随机变量不会影响大部分计量经济学理论的接过(特别是大样本情况下);
在进行回归分析之前,一般先做相关分析。
# 收入消费理论

# 回归函数

# 随机干扰项


随机干扰项:真实值与样本回归方程的估计值的差;
残差:真实值与总体回归方程的估计值的差;
随机感染项的来源:
- 遗漏或被排除的变量
- 数据的测量误差
- 错误的函数形式
- 纯粹的随机误差和无法预测的事件

偏回归系数

# 第二章 普通最小二乘法

# 线性回归模型的基本假设

以上假设也称为线性回归模型的经典假设或高斯(Gauss)假设,满足该假设的线性回归模型,也称为经典线性回归模型(Classical Linear Regression Model, CLRM)。
线性回归是指对估计参数为线性的一种回归(即估计参数只以一次方出现),对自变量 X 可以是或不是线性的;
# 估计量的性质

这三个准则被称作估计量的小样本性质,拥有这类性质的估计量称为最佳线性无偏估计量 (best liner unbiased estimator BLUE);
# 高斯 - 马尔可夫定理
在给定经典线性回归的假定下,最小二乘估计量是具有最小方差的线性无偏估计量即 BLUE。证明:略
# 判定系数

总平方和 = 回归平方和 + 残差平方和

判定系数 是解释变量个数的非减函数,即增加解释变量, 会增加或不变,但增加解释变量会降低自由度(自由度:观测样本个数减去待估参数的个数);

# 第三章 假设检验
# 假设检验的基本原理
假设检验是要确定一个准则(判定准则),以便决定拒绝或不拒绝某个原假设;
当拒绝原假设时,通常表述为统计上显著;反之,统计上不显著;


假设检验的判定准则:
判定准则是比较样本统计量与预先设定的临界值之间的大小;
参数估计值范围分为两个区域:拒绝域与接受域;
假设检验的两种常用方法:
1. 置信区间法
2. 显著性检验法
# 置信区间法
根据参数估计量的分布,在给定的置信水平(如 95%)下构造一个随机置信区间;若该随即区间覆盖原假设值,则不拒绝原假设,否则拒绝原假设。
置信区间的构造:



Std.Error :参数方差
# 显著性检验法(t 检验)



Prob. :对应其左侧一列 t 统计量的概率(即一般情况下,p<0.05 则认为其显著)
结论:
- 不能把 t 检验得出的统计显著性等同于理论的有效性;
- t 检验不能检验相应变量的相对重要性;
- 随着样本容量的增大,t 值会越来越大;
- 对于一个超大规模的样本而言,t 检验没用任何意义,因为你几乎可以拒绝任何原假设;
# F 检验
对多个假设的联立检验或对线性约束的假设检验不能用 t 检验,只能用 F 检验,可以检验方差的整体显著性。
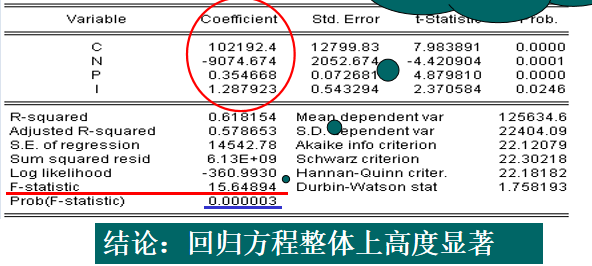
Prob (F-statistic): 模型的显著性,小于 0.05 为显著。
Wald Test(对参数进行具体检验)
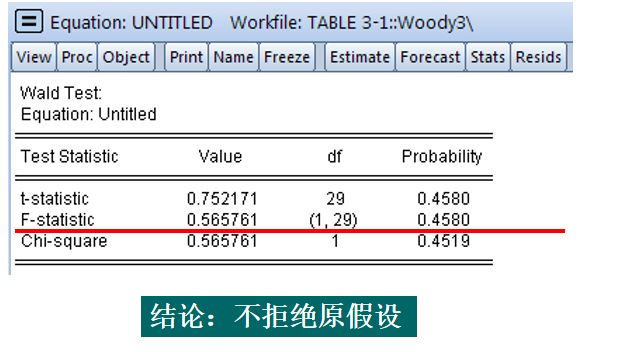
Probability: 假设正确的概率,小于 0.05 时拒绝原假设;
# 柯布 - 道格拉斯生产函数

# 邹检验
在时间序列回归中,模型的参数在整个样本期间内可能发生变化,邹检验由此而生,是 F 检验的重要应用。邹检验可以轻松推广到不止一次结构变动的情形。
EViews 操作
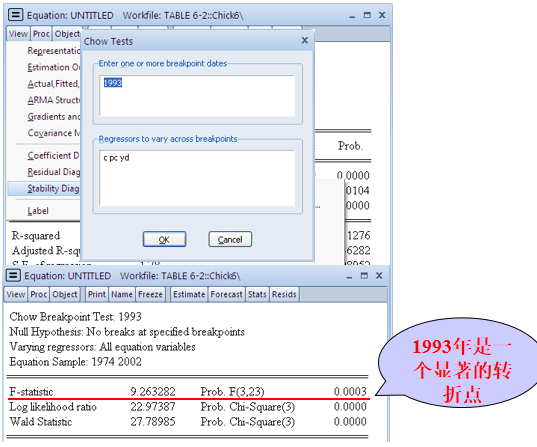
一些说明:
- 邹检验的假定:两个子时期回归的误差项是独立且具有同方差的正态分布变量;
- 邹检验只告诉我们不同子时期的回归方程是否有差别,并没有告诉我们差别来自于截距、斜率还是二者兼有;
- 邹检验假定我们知道结构转折点;
# 正态性检验
正态性检验是检验误差项是否为正太分布。
正太性的雅克 - 贝拉(Jarque-Bera)检验:
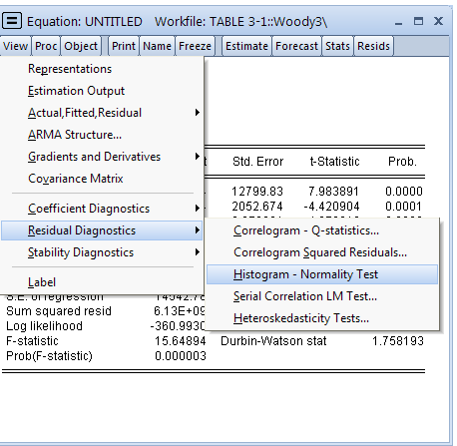
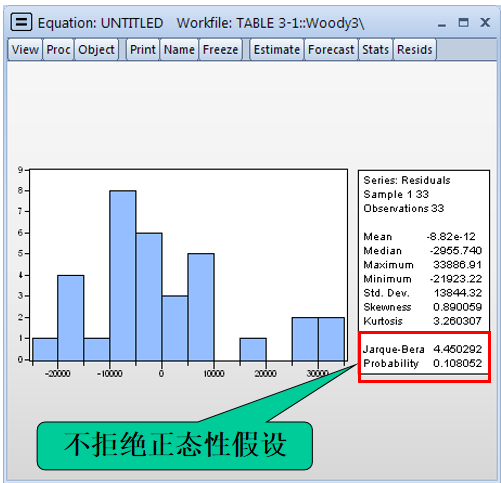
# 第四章 模型设定
一个正确的方程包含了:
- 正确的解释变量;
- 正确的函数形式;
- 正确的随机误差形式;
# 遗漏变量(设定偏误)
参数估计量有偏且 符号不一致 (方差变小);
EViews 上检查遗漏变量的操作方法:
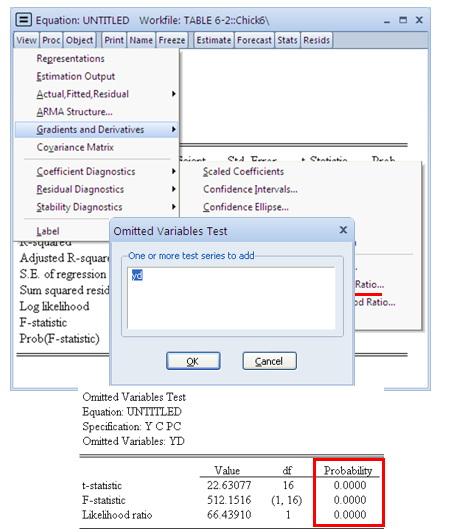
# 不相干变量
参数估计量无偏但非有效、 不显著 (方差增大,t 检验失效,拟合优度降低)
EViews 上检查不相干变量的操作方法:

# 模型选择准则
四个重要的模型设定准则:
1. 理论:变量在方程中的含义是不是含糊不清的,从理论上看是不是合理的?
2.t 检验:解释变量参数的估计值在预期假设下是不是显著的?
3. 调整的判定系数 或 AIC 和 SC: 将变量加入方程后,整体拟合优度是否有所改善?
4. 偏误:将变量加入方程后,其他变量参数是否有显著变化?

# AIC 与 SC


# 函数形式的选择
可线性化的非线性函数形式:
- 指数函数
- 对数函数
- 反函数形式
- 多项式形式
# 第五章 多重共线性
# 多重共线性的定义

多重共线性是一个程度问题而不是有无的问题,目前还没有一个被普遍接受的真正意义的检验多重共线性的统计量。
完全多重共线性只是一种极端的隐患,更常见的是出现不完全多重共线性;而只要是不完全多重共线性,用 OLS 仍可得到参数的估计值及其标准误差,并且是无偏,但尽管无偏,估计量的标准误差非常大即估计的精度很小。
# 不完全多重共线性的特征
偏回归系数的 t 值会降低,倾向于统计上不显著;
估计量(偏回归系数)对模型设定的变化非常敏感,估计系数可能出现非预期的符号或难以置信的数值;
虽然系数不显著,但总的拟合优度 却可能非常高;
可能出现每个偏回归系数的 t 值都不显著,但回归方程的 F 值却很显著。
# 多重共线性的检验与补救
检验方法:
- 变量之间的相关系数
- 方差膨胀因子(VIF)
补救方法:
- 剔除支配变量:支配变量 (dominant variable): 与被解释变量高度相关,以致于完全掩盖了方程中其他解释变量的影响 (如销售量与销售额);
- 增加样本容量:样本越大,估计越精确;
- 剔除多余的变量:潜在的理论假设作为剔除的主要依据;
# 差分法

# 比率转换法

# 无为而治法
剔除本应包含的解释变量会导致设定偏误。与遗漏变量造成的有偏估计相比较,较低的 t 统计值 (显著性) 似乎只是一个次要的问题。
只有当后果很严重 (参数估计值出现非预期的符号),才应该采取其他补救措施。
# 第六章 序列相关性
# 序列相关性的概念

# 自相关系数

# 序列相关性的类型
非纯序列相关:
通常由设定偏误导致,所谓模型设定偏误表现在模型中丢掉重要的变量或模型函数形式有错误即遗漏变量、不正确的函数形式;


纯序列相关:
- 时间序列数据:对同一总体的连续的观测很可能表现出某种系统的相关性,特别是连续观测的时间间隔很短时,如一周、一天、甚至一天内多次观测;
- 经济数据的周期性,如股票价格、GDP 等;
大多数经济时间数据都有一个明显的特点:惯性,表现在时间序列不同时间的前后关联上。
# 序列相关性的特征
# 序列相关性的检验
序列相关性检验的方法有很多种,但基本思路相同。

图示法
![]()
回归检验法:
![]()
# 杜宾 - 瓦森(DW)检验法![]()

DW 检验临界值 () 与三个参数有关:
①检验水平,②样本容量 n , ③原回归模型中解释变量个数 k(不包括常数项)。

若采用双侧侧检验,则结论为是否存在序列相关。
当 DW 值落在 “不确定” 区域时,两种处理方法:
- 加大样本容量或重新选取样本,重作 DW 检验。有时 DW 值会离开不确定区;
- 选用其它检验方法。
# 拉格朗日乘数检验(GB/LM)
拉格朗日乘数检验克服了 DW 检验的缺陷,适合于高阶序列相关以及模型中存在滞后被解释变量的情形。
它是由布劳殊(Breusch)与戈弗雷(Godfrey)于 1978 年提出的,也被称为 GB 检验。
对于模型 $$Y_i=\beta_0+\beta_1X_{1i}+\beta_2X_{2i}+\cdots+\beta_kX_{ki}+\mu$$
如果怀疑随机扰动项存在 P 阶序列相关:


拉格朗日乘数检验的 EViews 操作

# 序列相关性的补救
非纯序列相关:
- 正确的模型设定,特别是出现负的序列相关时;
纯序列相关:
广义最小二乘法:广义差分法(GLS)
EViews 操作:
![]()
![]()
AR 方法
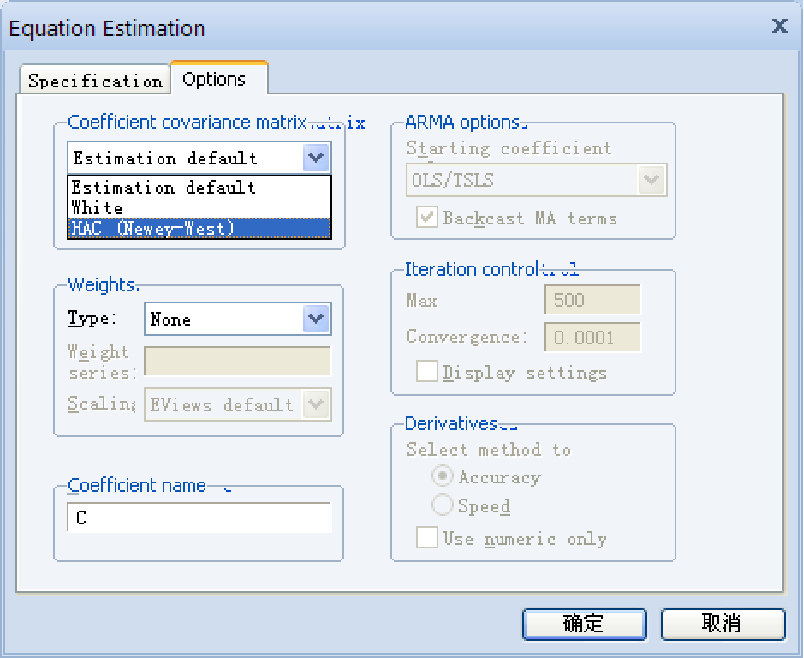
尼威 - 韦斯特(Newey-West HAC)方法
只修正标准误而不会改变系数的估计值
在大样本估计中,效果更好
绝大多数学术论文采用此种方法
EViews 操作:
![]()
![]()
![]()
经验方法:
- 采用时间序列数据作回归时,不对原模型进行序列相关检验,而是直接选择广义差分法或者 NW 法;
- 如果确实存在序列相关,则被有效地消除了;
- 如果不存在序列相关,则广义差分法或 NW 法等价于普通最小二乘法;
# 第七章 异方差性
# 异方差的概念
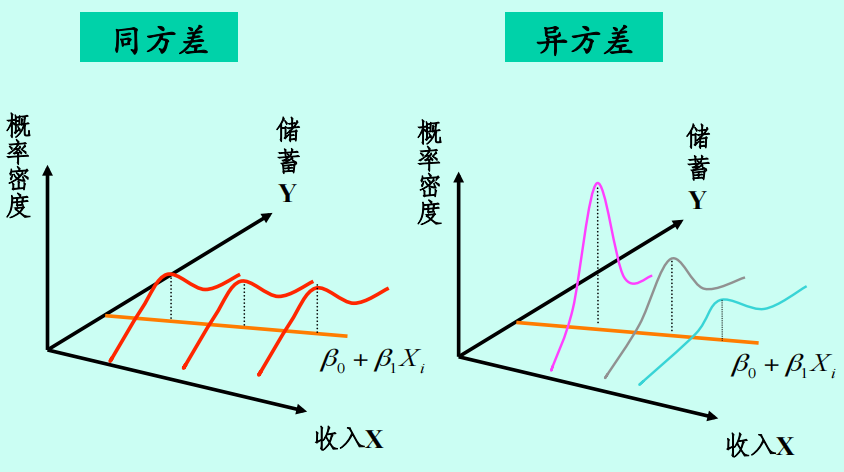

# 异方差的类型
** 非纯异方差:** 由模型设定偏误导致(如遗漏变量);
纯异方差:
- 横截面数据:被解释变量的取值差异较大、解释变量的偏态;
- 时间序列数据:学习效应、数据采集技术的变化
- 异常值
# 异方差的特征
- OLS 估计量仍是无偏的;
- OLS 估计量不再是有效的(即最小方差估计量);
- OLS 估计量的标准误是有偏的,且偏差通常是负的,意味着 OLS 通常会高估了参数的 t 值,导致原本不显著的变量可能变得显著;
综上:若存在异方差,OLS 估计的假设检验将变的不可靠。
# 异方差的检验
检验思路:
检验异⽅差,也就是检验随机误差项的方差与比例因子 Z 或解释变量 X 之间的相关性及其 “形式”;又因随机误差项方差的样本对应物是 OLS 的残差平方,因此所有的检验方法都基于残差平方。
异方差的检验方法:
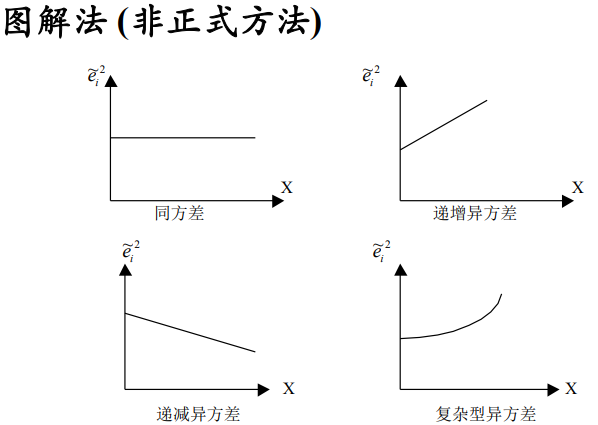
图解法
![]()
帕克检验
![]()
怀特检验(White)
基本思想:异方差来源于解释变量及其高次方。
EViews 操作:
![]()
# 异方差的补救
非纯异方差:
- 正确的模型设定
纯异方差:
- 首先考虑采用重新定义变量的方式
- 大样本情况:White 调整法
- 若能找到明确的比列因子(权重),则采用 WLS
# 加权最小二乘法 (WLS)

在实际操作中人们通常采用如下的经验方法:
不对原模型进行异方差检验,而是直接选择加权最小二乘法,尤其是采用截面数据作样本时。
如果确定存在异方差,则被有效地消除了;如果不存在异方差,则加权最小二乘法等价于普通最小二乘法。
# White 调整法
- 只修正标准误⽽不会改变系数的估计值;
- 在⼤样本估计中,效果更好;
- 绝⼤多数学术论⽂采用此种⽅法;
EViews 操作:
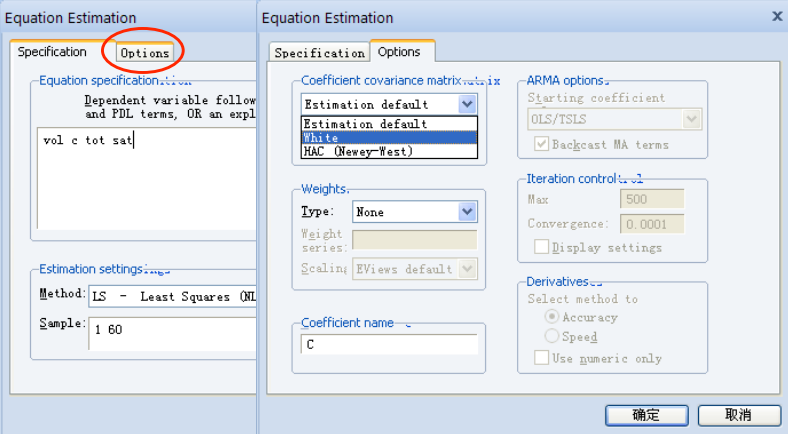
# 变换方程形式
一般采用对解释变量取对数的形式。
# 第八章 虚拟变量
# 虚拟变量概念

虚拟变量既可以作为解释变量,又可以作为被解释变量;虚拟应变量模型又称为概率模型、离散选择模型。
设置原则:
- 每⼀定性变量所需的虚拟变量个数要比该定性变量的类别数少 1,即如果有 m 个定性变量,只在模型中引⼊ m-1 个虚拟变量;
- 在同⼀个⽅程中,可以引⼊多个虚拟变量来考察多种定性因素的影响;
# 虚拟变量的引入

# 线性概率模型(LPM)


# Logit 模型

EViews 操作:
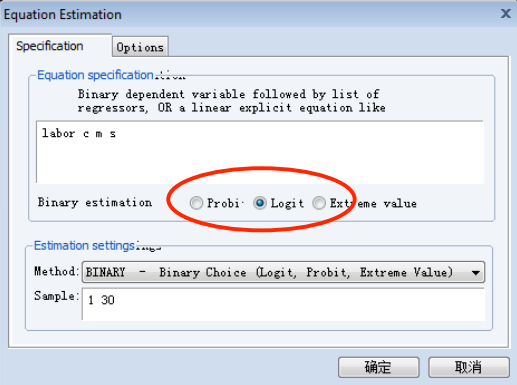

其参数估计值的解释:



# Probit 模型

EViews 操作:
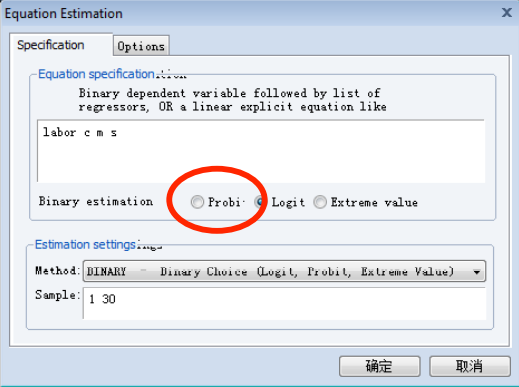
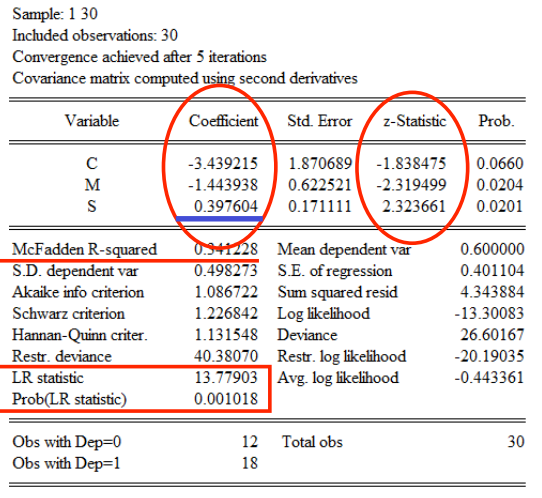
# 其它虚拟应变量模型
多元 Logit 模型:
- 被解释变量存在多种离散且⽆序的选择;
- 如择业的选择、交通⼯具的选择;
- 采用极⼤似然估计法,Eviews 中有示例程序;
序次 Logit 模型:
- 被解释变量存在多种离散且有序的选择;
- 如债券的信用评级、舆论调查结果;
- 采用极⼤似然估计法,Eviews 中可实现菜单操作;